ฟังก์ชัน

ฟังก์ชัน  จากข้อมูลนำเข้าในเซต  ไปยังผลที่เป็นไปได้ในเซต  (เขียนเป็น ) คือความสัมพันธ์ระหว่าง  กับ  ซึ่ง
สำหรับทุกค่า  ใน  จะมี  ใน  ซึ่ง 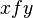 (  มีความสัมพันธ์  กับ ) นั่นคือ สำหรับค่านำเข้าแต่ละค่า จะมีผลลัพธ์ใน  อย่างน้อย  ผลลัพธ์เสมอ
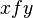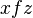ถ้า  และ  แล้ว 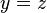 นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่สามารถมีผลลัพธ์หลายผลลัพธ์ได้
ค่านำเข้า  แต่ละค่า จากโดเมน จะมีผลลัพธ์  จากโคโดเมนเพียงค่าเดียว แทนด้วย 
จากนิยามข้างต้น เราสามารถเขียนอย่างสั้นๆได้ว่า ฟังก์ชันจาก  ไปยัง  คือเซตย่อย  ของผลคูณคาร์ทีเซียน  โดยที่แต่ละค่าของ  ใน  จะมี ใน  ที่แตกต่างกัน โดยที่คู่อันดับ  อยู่ใน 
เซตของฟังก์ชัน  ทุกฟังก์ชันแทนด้วย 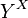 เรียกว่าปริภูมิฟังก์ชันสังเกตว่า 

ความสัมพันธ์ระหว่าง  กับ  ซึ่งเป็นไปตามเงื่อนไข (1) นั่นคือฟังก์ชันหลายค่าฟังก์ชันทุกฟังก์ชันเป็นฟังก์ชันหลายค่า แต่ฟังก์ชันหลายค่าไม่ทุกฟังก์ชันเป็นฟังก์ชัน ความสัมพันธ์ระหว่าง กับ  ซึ่งเป็นไปตามเงื่อนไข (2) นั่นคือฟังก์ชันบางส่วน ฟังก์ชันทุกฟังก์ชันเป็นฟังก์ชันบางส่วน แต่ฟังก์ชันบางส่วนไม่ทุกฟังก์ชันเป็นฟังก์ชัน "ฟังก์ชัน" คือความสัมพันธ์ที่เป็นไปตามเงื่อนไขทั้งสองเงื่อนไข
ดูเพิ่มเติม

เมทริกซ์

เมทริกซ์ คือกลุ่มของจำนวนหรือสมาชิกของริงใดๆ เขียนเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้าหรือจัตุรัส กล่าวคือเรียงเป็นแถวในแนวนอน และเรียงเป็นแถวในแนวตั้ง เรามักเขียนเมทริกซ์เป็นตารางที่ไม่มีเส้นแบ่งและเขียนวงเล็บคร่อมตารางไว้ (ไม่ว่าจะเป็นวงเล็บโค้งหรือวงเล็บเหลี่ยม) เช่น

เราเรียกแถวในแนวนอนของเมทริกซ์ว่า แถว เรียกแถวในแนวตั้งของเมทริกซ์ว่า หลัก และเรียกจำนวนแต่ละจำนวนเในเมทริกซ์ว่า สมาชิก ของเมทริกซ์ การกล่าวถึงสมาชิกของเมทริกซ์ จะต้องระบุตำแหน่งให้ถูกต้อง เช่น จากตัวอย่างข้างบน

สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 3 คือเลข 4

สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 2 คือเลข 15

สมาชิกที่อยู่ในแถวที่ 3 หลักที่ 1 คือเลข 5

เราเรียกเมทริกซ์ที่มี  แถว และ  หลัก เรียกว่า เมทริกซ์  เราเรียกจำนวน  และ  ว่า มิติ หรือ ขนาด ของเมทริกซ์ ดูเพิ่มเติม

เลขยกกำลัง

 เลขยกกำลัง คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
  

    ตัวอย่าง
                  25 เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
    

    และ         25   = 2x2x2x2x2  = 32

สมบัติของเลขยกกำลัง    

1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก          

                      

เช่น     23x 27x 29 = 2 (3 + 7 + 9) = 219

2. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก

กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n 

                                                                    

เช่น     412÷ 43=412-3  = 49

กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = n

                                                                     

นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a0 = 1

 เช่น      67÷ 67 = 67-7 = 60  = 1  หรือถ้า (-7)o = 1

 กรณีที่ 3เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n    

                                                                 

เช่น      =  1/ 54-9

นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว

             หรือ    

  เช่น               หรือ      

3.สมบัติอื่นๆของเลขยกกำลัง  

1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง     อ่านเพิ่มเติม